
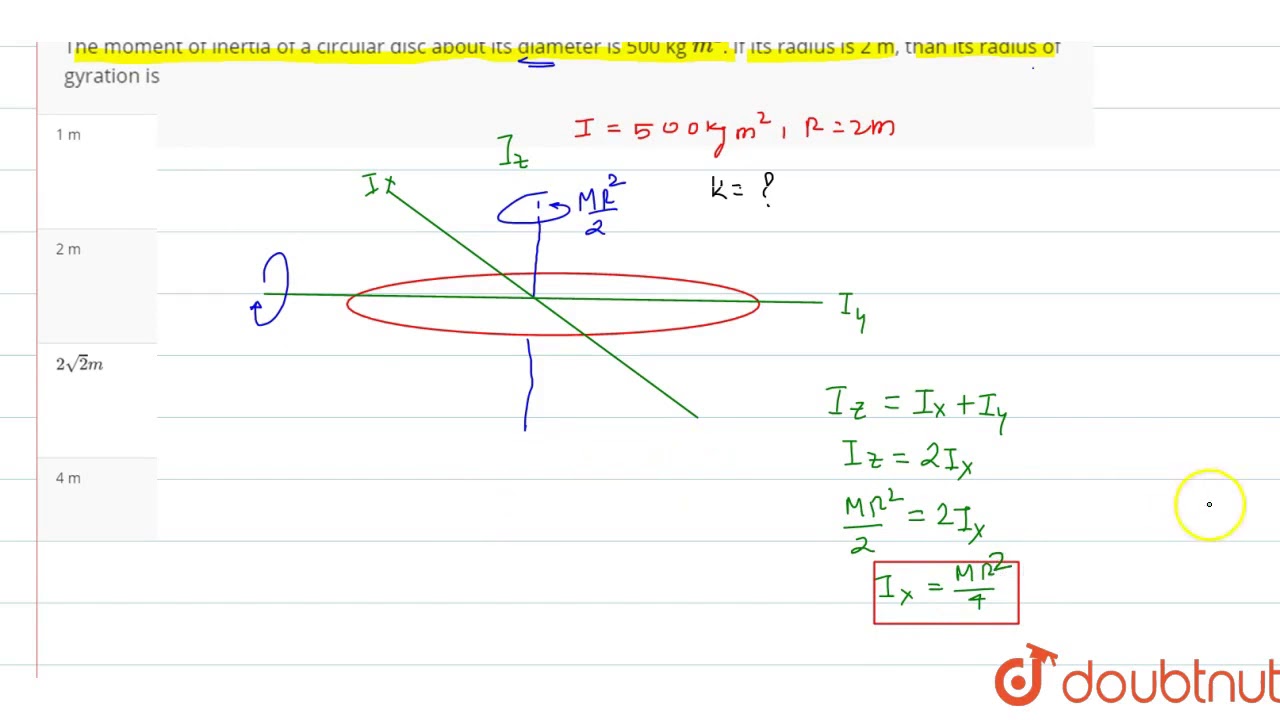
So this axis where this angle here is 35.62 is the angle which leaves this area as far away as possible from the axis and creates the maximum moment of inertia. So from here in a clockwise direction and angle 30, let's actually put a different color. So what we are saying is, to reach this point where the maximum moment of inertia is observed, we need to rotate in the clockwise direction by an angle 35.62. So 2 Theta max is the inverse tangent of 294.25 over 100, which is 71.23. The angle between the current point and the major axis, this angle, is the angle 2 Theta max. Let's find the axes which correspond to this maximum and minimum moment of inertia. So we obtained the principal moments of inertia. Similarly, the minimum moment of inertia is 850.33 minus one radius, minus 310.78. So this turns out to be the number 1161.11.
Circle moment of inertia formula plus#
The major, let's say the I_max, is 850.33, we send plus one radius, plus 310.78. Therefore, the first thing we do is to obtain the major and minor moments of inertia. The radius of the circle is nothing else but the square root of the distance from here to here it is 100 plus 294.25. Clearly, the center of the circle is at this point, which is halfway between these two points, so it's at 850.33. So we these two points, we construct a circle. So we replace the point with coordinates Ixx and Ixy up here, and similarly the point with coordinates Iyy, 750.3 and minus 294.25, over here. Now, the first thing using the data that we already obtained, we will construct more circle. Let's say, with respect to an axis which is 10 degrees in this direction. What we will do, we will try to calculate the moment of inertia with respect to a rotated axes. We actually calculated in earlier lecture the moments of inertia for this particular shape.
So let us look at an example of an L shape. You will have an exciting and interactive learning experience online! View Syllabus Katafygiotis is going to write and sketch with color markers directly on the board while facing you. The content will be primarily delivered using light board. Non engineering disciplines may also find the course very useful, from archaeologist who are concerned about the stability of their excavation sites to dentists interested in understanding the forces transmitted through dental bridges, to orthopedic surgeons concerned about the forces transmitted through the spine, or a hip or knee joint. This course is suitable for learners with interest in different Engineering disciplines such as civil engineering, architecture, mechanical engineering, aerospace.
Circle moment of inertia formula how to#
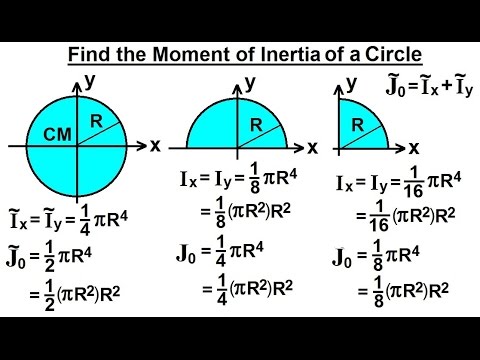
You will also learn how to calculate the reaction forces as well as the internal forces experienced throughout the structure so that later you can properly design and size the foundation and the members of the structure to assure the structure’s safety and serviceability. the conditions under which it remains stationary or moves with a constant velocity. In this course, you will learn the conditions under which an object or a structure subjected to time-invariant (static) forces is in equilibrium - i.e. So that you don’t get confused about how the values of Ixx and Iyy are computed, we’ve included the formulas for all the shapes utilised in this calculator below.Statics is the most fundamental course in Mechanics. Moment of Inertia of Different Geometric Shapes of Plywood SheetsĪlso Try : Sod Calculator – Estimate the Cost & Nos. To compute the Ixx and Iyy, you only need to enter a few measurements of the shapes.Īlso Try : Plywood Calculator – Estimate the Cost and Nos.The moment of inertia of various geometric shapes about their centroidal axis can be calculated.This online calculator is really simple to use.Steps to use this grade calculator are mentioned below: It is defined as the distance from a particular reference at which the entire mass or area of the body is supposed to be concentrated in order to produce the same value of ‘I’. The radius of gyration is denoted by ‘k’ in the preceding equation. If the area of the figure is considered instead of the mass, the moment of inertia of the area is given by:

etc are the distances between two points on a fixed line, as shown in the picture, then the mass moment of inertia of the entire body is given by: Let it be made up of minuscule particles with masses m1, m2, m3, and so on.


 0 kommentar(er)
0 kommentar(er)
